Building Variational Auto-Encoders in TensorFlow

Variational Auto-Encoders (VAEs) are powerful models for learning low-dimensional representations of your data. TensorFlow’s distributions package provides an easy way to implement different kinds of VAEs.

In this post, I will walk you through the steps for training a simple VAE on MNIST, focusing mainly on the implementation. Please take a look at Kevin Frans’ post for a higher-level overview.

Defining the Network

A VAE consist of three components: an encoder \(q(z\vert x)\), a prior \(p(z)\), and a decoder \(p(x\vert z)\).

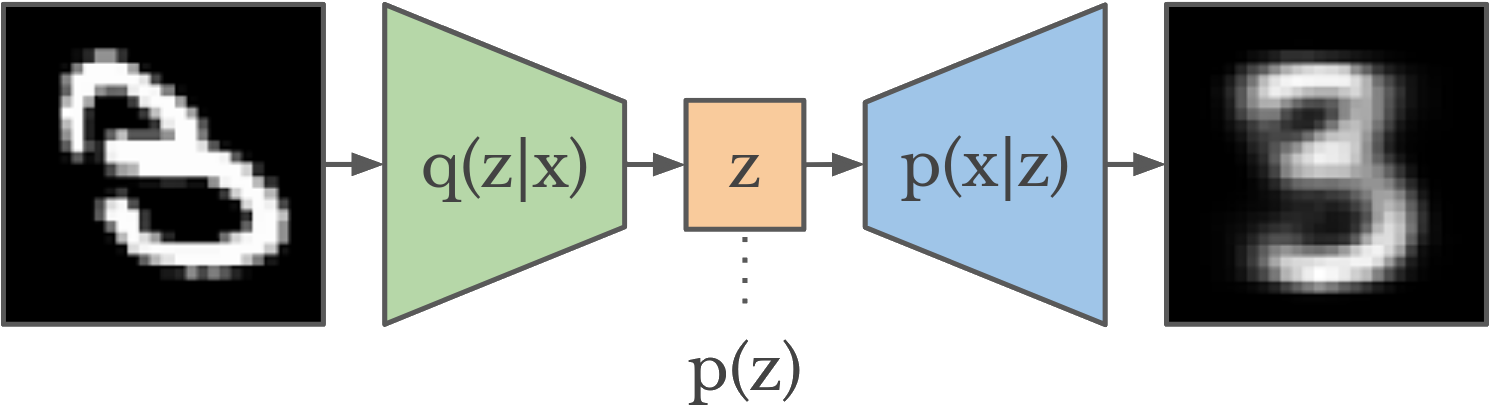
The encoder maps an image to a proposed distribution over plausible codes for that image. This distribution is also called the posterior, since it reflects our belief of what the code should be for (i.e. after seeing) a given image.

import tensorflow as tf
tfd = tf.contrib.distributions

def make_encoder(data, code_size):
  x = tf.layers.flatten(data)
  x = tf.layers.dense(x, 200, tf.nn.relu)
  x = tf.layers.dense(x, 200, tf.nn.relu)
  loc = tf.layers.dense(x, code_size)
  scale = tf.layers.dense(x, code_size, tf.nn.softplus)
  return tfd.MultivariateNormalDiag(loc, scale)

The prior is fixed and defines what distribution of codes we would expect. This provides a soft restriction on what codes the VAE can use. It is often just a Normal distribution with zero mean and unit variance.

def make_prior(code_size):
  loc = tf.zeros(code_size)
  scale = tf.ones(code_size)
  return tfd.MultivariateNormalDiag(loc, scale)

The decoder takes a code and maps it back to a distribution of images that are plausible for the code. It allows us to reconstruct images, or to generate new images for any code we choose.

import numpy as np

def make_decoder(code, data_shape):
  x = code
  x = tf.layers.dense(x, 200, tf.nn.relu)
  x = tf.layers.dense(x, 200, tf.nn.relu)
  logit = tf.layers.dense(x, np.prod(data_shape))
  logit = tf.reshape(logit, [-1] + data_shape)
  return tfd.Independent(tfd.Bernoulli(logit), 2)

Here, we use a Bernoulli distribution for the data, modeling pixels as binary values. Depending on the type and domain of your data, you may want to model it in a different way, for example again as a Normal distribution.

The tfd.Independent(..., 2) tells TensorFlow that the inner two dimensions, width and height in our case, belong to the same data point, even though they have independent parameters. This allows us to evaluate the probability of an image under the distribution, not just individual pixels.

Reusing Model Parts

We would like to use the decoder network twice, for computing the reconstruction loss described in the next section, as well as to decoder some randomly sampled codes for visualization.

In TensorFlow, if you call a network function twice, it will create two separate networks. TensorFlow templates allow you to wrap a function so that multiple calls to it will reuse the same network parameters.

make_encoder = tf.make_template('encoder', make_encoder)
make_decoder = tf.make_template('decoder', make_decoder)

The prior has no trainable parameters, so we do not need to wrap it into a template.

Defining the Loss

We would like to find the network parameters that assign the highest likelihood to our data set. However, the likelihood of a data point depends on the best code for it, which we don’t know during training.

Instead, we train the model using the evidence lower bound (ELBO), an approximation to the data likelihood.

The important detail here is that the ELBO only uses the likelihood of a data point given our current estimate of its code, which we can sample.

data = tf.placeholder(tf.float32, [None, 28, 28])

prior = make_prior(code_size=2)
posterior = make_encoder(data, code_size=2)
code = posterior.sample()

likelihood = make_decoder(code, [28, 28]).log_prob(data)
divergence = tfd.kl_divergence(posterior, prior)
elbo = tf.reduce_mean(likelihood - divergence)

An intuitive interpretation is that maximizing the ELBO maximizes the likelihood of the data given the current codes, while encouraging the codes to be close to our prior belief of how codes should look like.

Running the Training

We just maximize the ELBO using gradient descent. This works because the sampling operations are implemented using the reparameterization trick internally, so that TensorFlow can backpropagate through them.

optimize = tf.train.AdamOptimizer(0.001).minimize(-elbo)

Moreover, we sample a few random codes from the prior to visualize the corresponding images that the VAE has learned. This is why we used tf.make_template() above, allowing us to call the decoder network again.

samples = make_decoder(prior.sample(10), [28, 28]).mean()

Finally, we load the data and create a session to run the training:

from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets('MNIST_data/')

with tf.train.MonitoredSession() as sess:
  for epoch in range(20):
    test_elbo, test_codes, test_samples = sess.run(
        [elbo, code, samples], {data: mnist.test.images})
    print('Epoch', epoch, 'elbo', test_elbo)
    plot_codes(test_codes)
    plot_sample(test_samples)
    for _ in range(600):
      sess.run(optimize, {data: mnist.train.next_batch(100)[0]})

That’s it! If you want to play around with the code, take a look at the full code example. It also contains the plotting omitted in this post. Here are the latent codes, color-coded by the labels, as well as the decoded samples from the prior for the first few epochs of training.

As you can see, the latent space quickly separates into clusters for some of the different digits. If you use more dimensions for the code and larger networks, you will also see the generated images getting sharper.

Conclusion

We’ve learned to build a VAE in TensorFlow and trained it on MNIST digits. As a next step, you can run the code yourself and extend it, for example using a CNN encoder and deconv decoder. As always, if you have any question, please ask them below.

You can use this post under the open CC BY-SA 3.0 license and cite it as:

@misc{hafner2018tfdistvae,
  author = {Hafner, Danijar},
  title = {Building Variational Auto-Encoders in TensorFlow},
  year = {2018},
  howpublished = {Blog post},
  url = {https://danijar.com/building-variational-auto-encoders-in-tensorflow/}
}